Grado Undécimo: Desigualdades de valor absoluto

-

Desigualdades de valor absoluto


Una desigualdad de valor absoluto es una desigualdad que tiene un signo de valor absoluto con una variable dentro.



Desigualdades de valor absoluto (<):

La desigualdad | x | < 4 significa que la distancia entre x y 0 es menor que 4.
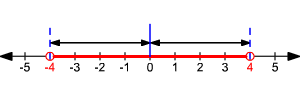
Así, x > -4 Y x < 4. El conjunto solución es  .
Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
La solución es la intersección de las soluciones de estos dos casos.
En otras palabras, para cualesquiera números reales a y b , si | a | < b , entonces a < b Y a > - b .
Ejemplo 1 :
Resuelva y grafique.
| x – 7| < 3
Para resolver este tipo de desigualdad, necesitamos descomponerla en una desigualdad compuesta .
x – 7 < 3 Y x – 7 > –3
–3 < x – 7 < 3
Sume 7 en cada expresión.
-3 + 7 < x - 7 + 7 < 3 + 7
4 < x <10
La gráfica se vería así:

Desigualdades de valor absoluto (>):

La desigualdad | x | > 4 significa que la distancia entre x y 0 es mayor que 4.
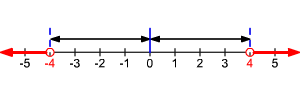
Así, x < -4 O x > 4. El conjunto solución es  .
Cuando se resuelven desigualdes de valor absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de valor absoluto es negativa.
En otras palabras, para cualesquiera números reales a y b , si | a | > b , entonces a > b O a < - b .


Ejemplo 2 :
Resuelva y gráfique.
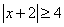
Separe en dos desigualdades.
Reste 2 de cada lado en cada desigualdad.
La gráfica se vería así:




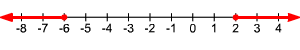
Test: Por Favor ingresar con el siguiente código, luego identificarse con el curso Apellido Nombre por ejemplo: 1111 Suarez Alejandro 
CÓDIGO DEL JUEGO
382215

Pida a sus estudiantes que se unan al juego con este código en https://join.quizizz.com

Comentarios

Publicar un comentario

Entradas populares de este blog

Función Inyectiva, Sobreyectiva y Biyectiva

-
Imagen
Función Inyectiva La función f es inyectiva si cada elemento del conjunto final Y tiene como máximo un elemento del conjunto inicial X al que le corresponde. Es decir, no pueden haber más de un valor de X que tenga la misma imagen y . En términos matemáticos, una función f es inyectiva si: Ejemplo de función inyectiva La función f ( x ) = 2 x +1 es inyectiva . Veamos que se cumple la condición de inyectividad: En efecto, si x y y tienen la misma imagen , necesariamente deben ser el mismo elemento. Por lo tanto, f es inyectiva. Función sobreyectiva Una función f es sobreyectiva (o suprayectiva ) si todo elemento del conjunto final Y tiene al menos un elemento del conjunto inicial X al que le corresponde. Es decir, una función es sobreyectiva si el recorrido de la función es el conjunto final Y . En términos matemáticos, una función f es sobreyectiva si: Ejemplo de función sobreyectiva La función...
Leer más

UNDÉCIMO: LIMITES TRIGONOMETRICOS

-
Imagen
Propiedades: Para llevar acabo la resolución de los límites algebraicos, es necesario conocer las propiedades de los límites. Problema 1.- Resolver el siguiente límite trigonométrico Solución: Como el tema que estamos viendo es sobre indeterminación de la forma 0/0, es lógico que al evaluar obtengamos la indeterminación, así que lo primero que haremos es pensar un poco en lo que tenemos y tener en cuenta que si tenemos: Lo más accesible, es recurrir a su complemento para formar una diferencia de cuadrados en el denominador pues es más fácil llegar así a un límite notable, entonces hacemos lo siguiente: Haciendo la operación, tenemos. De la identidad pitagórica nosotros observamos que: Despejando a seno cuadrado de x. Pero esto no se parece a lo que obtuvimos en el denominador de nuestro límite, peeeeero hay una solución y eso es factorizar el signo para que el límite nos quede de la siguiente forma: Ahora hacemos el cambio ...
Leer más