Función lineal

DEFINICIÓN DEFUNCIÓN LINEAL

La noción de función tiene diversos usos. En esta ocasión, nos vamos a centrar en la función matemática: la relación que se establece entre dos conjuntos, a través de la cual a cada elemento del primer conjunto se le asigna solo un elemento del segundo conjunto, o ninguno.

Con esto en claro, podemos avanzar en la idea de función lineal. Así se denomina a la función matemática compuesta por variables de primer grado. Cabe destacar que una variable es una magnitud que, en el marco de un cierto conjunto, puede adoptar cualquiera de los valores posibles.

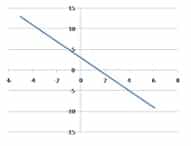
Las funciones lineales se representan con una línea recta en el plano cartesiano. Es importante tener en cuenta que lo que hacen las funciones, en definitiva, es expresar una relación entre variables, pudiéndose desarrollar modelos matemáticos que representen este vínculo.

El conjunto de partida o conjunto inicial se lo denomina dominio, mientras que al conjunto de llegada o conjunto final se lo llama codominio. Las variables independientes forman parte del dominio; las variables dependientes, del codominio. Cuando a los cambios iguales de una variable independiente le corresponden variaciones iguales de la variable dependiente, se habla de función lineal.

Y = X + 2 es un ejemplo de función lineal. Supongamos que en el dominio tenemos los valores 2, 5 y 7. Si la función señala que Y es igual a X + 2, en el codominio encontraremos los valores 4, 7 y 9:

X + 2 = Y
2 + 2 = 4
5 + 2 = 7
7 + 2 = 9

Al llevar esta función lineal a un gráfico en coordenadas cartesianas, nos encontraremos con una línea recta creciente: a medida que crecen los valores de X, crecen proporcionalmente los valores de Y.

Pendiente de una recta

La pendiente es la inclinación de la recta con respecto al eje de abscisas.

Se denota con la letra m.

Si m > 0 la función es creciente y ángulo que forma la recta con la parte positiva del eje OX es agudo.

Si m < 0 la función es decreciente y ángulo que forma la recta con la parte positiva del eje OX es obtuso.

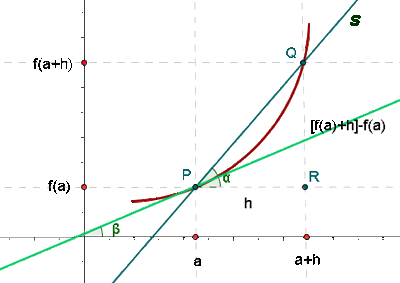
La pendiente de una recta es la tangente del ángulo que forma la recta con la dirección positiva del eje de abscisas.

Cálculo de la pendiente

Pendiente dado el ángulo

Pendiente dado el vector director de la recta

Pendiente dados dos puntos

Pendiente dada la ecuación de la recta.

Ejemplos

La pendiente de la recta que pasa por los puntos A(2, 1), B(4, 7) es:

La recta que pasa por los puntos A(1, 2), B(1, 7) no tiene pendiente, ya que la división por 0 no está definida.

La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto.

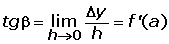
Vídeos de apoyo

Documento de interés 


Test 


Biografía

https://definicion.de/funcion-lineal/

http://recursostic.educacion.es/descartes/web/materiales_didacticos/EDAD_3eso_funciones_lineales/3eso_quincena10.pdf

https://www.ditutor.com/funciones/pendiente-recta.html