Buenos días,

Hoy vamos a abordar el interesante tema del Dominio y Rango de una función

Introducción

Las relaciones y las funciones describen la interacción entre variables que están ligadas. Estas relaciones incluyen valores independientes y entradas, que son las variables que pueden ser manipuladas por las circunstancias. También incluyen valores dependientes y salidas, que son las variables determinadas por los valores independientes. Existe otro par de componentes que debemos considerar cuando hablamos de relaciones, se llaman dominio y rango.

El dominio de una función o relación es el conjunto de todos los valores independientes posibles que una relación puede tener. Es la colección de todas las entradas posibles.

El rango de una función o relación es el conjunto de todos los valores dependientes posibles que la relación puede producir. Es la colección de todas las salidas posibles.

Al poner a todas las entradas y las salidas en grupos separados, el dominio y el rango nos permiten encontrar y explorar patrones en cada tipo de variable.

Dominio y Rango: Ejemplos y Notación

El dominio y el rango de una función están normalmente limitados por la naturaleza de la relación. Por ejemplo, considera la función de tiempo y altura que ocurre cuando lanzas una pelota al aire y luego la atrapas. El tiempo es la entrada, la altura es la salida. El dominio es cada valor de tiempo durante el lanzamiento, e inicia desde el instante en que la pelota abandona tu mano hasta el instante que la pelota regresa a ella. El tiempo antes de que la lances y el tiempo después de que la atrapas es irrelevante, ya que la función sólo aplica para la duración del lanzamiento. Digamos que la pelota estuvo en el aire durante 10 segundos — en ese caso, el dominio es 0-10 segundos. Ya que el tiempo transcurre continuamente durante éste intervalo, no podemos escribir cada posible salida, sólo el valor inicial y el valor final.

El rango es cada altura de la pelota mientras está en el aire, e incluye todas las alturas, desde la altura de tu mano cuando lanzaste la pelota, hasta el punto más alto alcanzado antes que ésta empezara a caer. Si tu mando estaba a 3 pies del suelo cuando aventaste y atrapaste la pelota, y la distancia más alta que alcanzó fue de 12 pies también con respecto al suelo, entonces el rango es de 3-12 pies. Ya que la altura cambia constantemente durante éste intervalo, no podemos escribir cada posible salida, sólo el valor inicial y el valor final.

Ahora veamos otro ejemplo de dominio y rango, Aquí hay una serie de figuras, cada una de ellas formada por cuadrados.

Podemos crear una función a partir de éstas usando el número de la figura como la entrada, y el número de cuadros que la conforman como la salida.

Una entrada de 1 tiene una salida de 1, ya que la figura 1 tiene sólo un cuadrado. Una entrada de 2 tiene una salida de 5, ya que la figura 2 contiene 5 cuadrados. Una entrada de 3, produce una salida de 9, ya que la figura 3 está formada de 9 cuadros. El dominio de ésta función se obtiene contando el número de entradas 1, 2, 3 que identifican cada una de las figuras usadas. Las entradas de ésta función son valores discretos, o valores que cambian en incrementos y no continuamente como la función del lanzamiento de la pelota. Sólo hay 3 figuras y por lo tanto las únicas posibles entradas son 1, 2, y 3. Entonces, el dominio de ésta función es 1, 2, 3. Podemos agrupar ésta lista de valores dentro de corchetes para indicar que forman un conjunto.

Dominio: {1, 2, 3}

El rango es el número de cuadros en cada figura. Las figuras tienen sólo 1, 5, o 9 cuadros, y ése es el rango. No hay ninguna figura que tenga 2 o 3.5 o cualquier otro número de cuadros. Como el dominio, el rango esta hecho de un conjunto de valores discretos.

Rango: {1, 5, 9}

Hemos limitado la entrada y la salida a 3 cada una porque sólo nos proporcionaron 3 figuras. ¿Cómo sería la notación del dominio y del rango si nos hubieran dicho que el patrón continuaría indefinidamente? ¡Fácil! Sólo añadimos tres puntos al final del conjunto de valores, para indicar que la secuencia continúa, así:

Dominio: {1, 2, 3, …}

Rango: {1, 5, 9, …}

Jamie vende pasteles caseros en $15 cada uno. La cantidad de dinero que gana es una función de cuántos pasteles puede vender: $0 si no vende ninguno, $15 si sólo vende uno, $30 si vende 2, y así sucesivamente. ¿Cuáles son el dominio y el rango de la función?

A) Dominio: {0, 15, 30, …} Rango: {0, 1, 2, …}

B) Dominio: {0, 1, 2, …} Rango: {0, 15, 30, …}

C) Dominio: {0, 1, 2} Rango: {0, 15, 30}

D) Dominio: todos los números mayores o iguales a 0

Mostrar/Ocultar la Respuesta

Dominio y Rango: Tablas y Conjuntos de Pares Ordenados

Las relaciones también pueden ser mostradas como tablas o como conjuntos de pares ordenados. Encontrar el dominio y el rango en estas situaciones es simple, siempre y cuando recordemos qué es lo que significan los términos. Si una relación matemática es dada en una tabla, los valores independientes generalmente se enlistan en la columna izquierda, mientras que los valores dependientes normalmente se ponen en la columna derecha.

Valor Independiente	Valor Dependiente
-1	7
2	-3
5	6
9	4

El dominio se puede encontrar al leer la primera columna {-1, 2, 5, 9}. El rango es todos los valores de la segunda columna {7, -3, 6, 4}.

Cuando se trata de conjuntos de pares ordenados, simplemente necesitamos separar los pares en coordenadas x y coordenadas y. Ya que las coordenadas x conforman los valores independientes, nos dan el dominio. Las coordenadas y son los valores dependientes, lo que significa que son el rango. Intentémoslo.

En el conjunto de pares ordenados {(-2, 0), (0, 6), (2, 12), (4, 18)}, el dominio es el conjunto de los primeros números de cada par (esos son las coordenadas x): {-2, 0, 2, 4}. El rango es el conjunto de los número que conforman el segundo componente de cada par (esos son las coordenadas y): {0, 6, 12, 18}.

{(-2, 0), (0, 6), (2, 12), (4, 18)}

Dominio: {-2, 0, 2, 4}.

Rango: {0, 6, 12, 18}

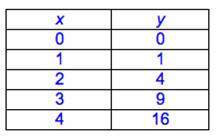
Esta tabla describe y como una función de x.

¿Cuál de las siguientes respuestas describe correctamente el valor de 2?

A) Es parte del rango.

B) Es una salida.

C) Es un valor dependiente.

D) Es parte del dominio.

Mostrar/Ocultar la Respuesta

Dominio y Rango: Gráficas

También podemos representar funciones y relaciones con gráficas. La cantidad independiente normalmente se grafica en el eje horizontal (x) — lo que significa que los puntos en la coordenada x son el dominio. Como la cantidad dependiente normalmente se grafica en el eje vertical (y) , las coordenadas y conforman el rango. Veamos algunas gráficas para entender cómo funciona esto.

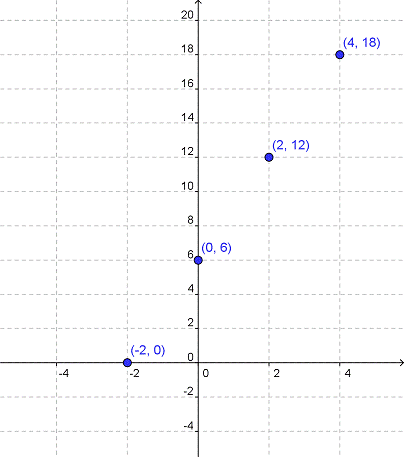
Primero, examina la gráfica de puntos discretos. Los únicos valores que conocemos que satisfacen la ecuación son los marcados con puntos. Simplemente leemos las coordenadas x, y los colocamos en un conjunto de valores que representan el dominio. Luego leemos las coordenadas y, y los ponemos en el rango. Para ésta gráfica, el dominio es {-2, 0, 2, 4}. Y el rango es {0, 6, 12, 18}.

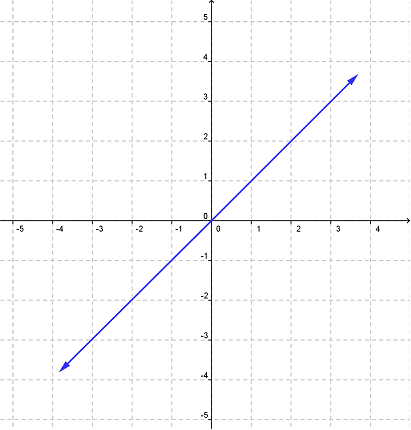
Ahora veamos un tipo de gráfica diferente, en el cual la función es una recta continua, que se extiende indefinidamente en ambas direcciones. Esto significa que hay un número infinito de valores que son parte de la función. Para ésta función, no hay restricciones para el dominio ni para el rango. Cualquier número real puede ser una entrada o una salida. Esto significa que todos los números, enteros, fracciones y otros números racionales, incluso números irracionales, son parte del dominio y parte del rango. Como no podemos escribir todas estas posibilidades, simplemente decimos que el dominio y el rango son todos los números reales.

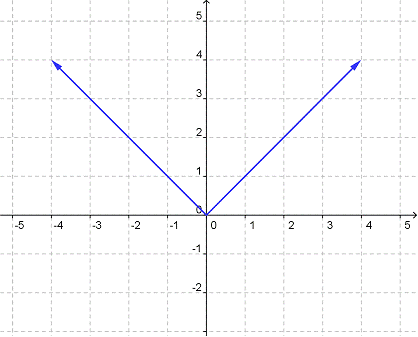
En algunas situaciones sólo uno de los dos, el dominio o el rango, está restringido. Considera la gráfica del valor absoluto de la función, y = |x|. La línea se extiende indefinidamente en ambas direcciones sobre el eje x, por lo que el dominio son todos los números reales. Sin embargo, como el valor absoluto transforma cualquier valor negativo en uno positivo, no existen valores negativos en el rango. El rango está formado de todos los números reales mayores o iguales a 0 — aunque siguen siendo demasiados como para escribirlos todos.

Dominio y rango de una función

El dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma.

(En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución. Quizá también estos han sido llamados la entrada y salida de la función.)

Ejemplo 1:

Considere la función mostrada en el diagrama.

Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D .

El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay letra en el dominio que se enlace con el 2.

Ejemplo 2:

El dominio de la función

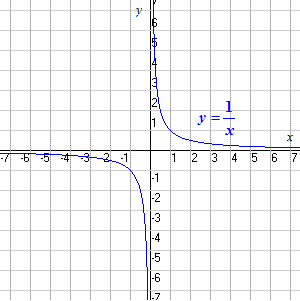
f ( x ) = 1/ x

es todos los números reales excepto el cero (ya que en x = 0, la función no está definida: la división entre cero no está permitida!).

El rango también es todos los números reales excepto el cero. Puede ver que hay algún punto en la curva para cada valor de y excepto para y = 0.

Los dominios pueden también estar explícitamente especificados, si hay valores para los cuales la función pudiera estar definida, pero que no deseamos considerarlos por alguna razón.

Ejemplo 3:

La notación siguiente muestra que el dominio de la función está restringido al intervalo (–1, 1).

f ( x ) = x 2 , –1

La gráfica de esta función es como se muestra. Dese cuenta de los círculos abiertos, que muestran que la función no está definida en x= –1 y x = 1. Los valores del rango de y desde 0 hasta el 1 (incluyendo el 0, pero no incluyendo el 1). Así el rango de la función es

y < 1.

Esta información fue extraída de Varsitytutors

.........................................................................................
https://www.youtube.com/watch?v=qOCMPXoxJyg