GRADO UNDÉCIMO: LÍMITES AL INFINO

LÍMITES AL INFINITO 

Un límite al infinito es aquel al que tiende f(x) cuando la variable x se hace tan grande, tanto en positivo como en negativo, como queramos. Entonces la función f(x) puede tender a un valor finito o puede diverger a infinito (límite infinito).

Veamos un caso, con un límite al infinito en la siguiente función:

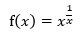
Su límite cuando la variable tiende a 2 es:

Se puede comprobar si damos valores a la x cada vez más cercanos a +∞. Como se ve en el siguiente cuadro, el límite tiende a 1:

Visto en esta gráfica:

Veamos los tipos de límites al infinito que se pueden presentar.

Tipos de límites al infinito

Límite finito L cuando x → +∞

Existe un límite finito L cuando la variable x tiende a +∞ si, en un entorno pequeño alrededor de L se cumple que, dentro de ese entorno, f(a) > f(b) (siendo a < b).

como se ve en la figura:

Límite finito L cuando x → -∞

Existe un límite finito L cuando la variable x tiende a -∞ si, en un entorno pequeño alrededor de L se cumple que, dentro de ese entorno, f(b) < f(a) (siendo b < a).

Como se ve en la figura:

Ahora los tipos de límites al infinito en los que el valor del límite es un límite infinito.

Cuando x → +∞ y el límite = +∞

Si en f(x) y x → +∞, las imágenes de la función se hacen infinitamente grandes (positivas).

Cuando x → +∞ y el límite = -∞

Si en f(x) y x → +∞, las imágenes de la función se hacen infinitamente grandes y negativas.

Cuando x → -∞ y el límite = +∞

Si en f(x) y x → -∞, las imágenes de la función se hacen infinitamente grandes (positivas).

Cuando x → -∞ y el límite = -∞

Si en f(x) y x → -∞, las imágenes de la función se hacen infinitamente grandes y negativas.

VÍDEOS DE APOYO