GRADO SÉPTIMO: Producto Cartesiano, Relaciones y Funciones

Producto Cartesiano

En matemáticas, el producto cartesiano de dos conjuntos es una operación, que resulta en otro conjunto, cuyos elementosson todos los pares ordenados que pueden formarse de forma que el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto.

El producto cartesiano recibe su nombre de René Descartes, cuya formulación de la geometría analítica dio origen a este concepto

Ejemplo

Por ejemplo, dados los conjuntos:

${\displaystyle A=\{1,2,3,4\}}$

y

${\displaystyle B=\{a,b\}}$

su producto cartesiano de A por B es:

${\displaystyle {\begin{array}{r|cccc}b&(1,b)&(2,b)&(3,b)&(4,b)\\a&(1,a)&(2,a)&(3,a)&(4,a)\\\hline A\times B&1&2&3&4\\\end{array}}}$

que se representa:

${\displaystyle A\times B=\{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b),(4,a),(4,b)\}}$

y el producto cartesiano de B por A es:

${\displaystyle {\begin{array}{r|cc}4&(a,4)&(b,4)\\3&(a,3)&(b,3)\\2&(a,2)&(b,2)\\1&(a,1)&(b,1)\\\hline B\times A&a&b\\\end{array}}}$

que se representa:

${\displaystyle B\times A=\{(a,1),(a,2),(a,3),(a,4),(b,1),(b,2),(b,3),(b,4)\}}$

Ver que:

${\displaystyle (1,a)\neq (a,1)}$

Dado que son pares ordenados.

Definición

Un par ordenado es una colección de dos objetos distinguidos como primero y segundo, y se denota como (a, b), donde a es el «primer elemento» y b el «segundo elemento». Dados dos conjuntos A y B, su producto cartesiano es el conjunto de todos los pares ordenados que pueden formarse con estos dos conjuntos:

El producto cartesiano de A y B es el conjunto A × B cuyos elementos son los pares ordenados (a, b), donde a es un elemento de A y b un elemento de B: ${\displaystyle A\times B=\{(a,b):a\in A\;\;{\text{y}}\;\;b\in B\}}$

Puede definirse entonces el cuadrado cartesiano de un conjunto como A² = A × A.

El conjunto Z² puede visualizarse como el conjunto de puntos en el plano cuyas coordenadas son números enteros.

Ejemplo

Números enteros

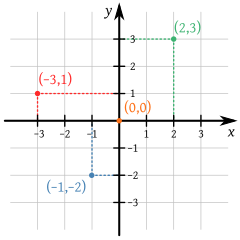
Sea también el conjunto de todos los números enteros Z = {..., −2, −1, 0, +1, +2, ...}. El producto cartesiano de Z consigo mismo es Z² = Z × Z = { (0,0), (0, +1), (0, −1), (0, +2), ..., (+1, 0), ... (−1, 0), ... }, es decir, el conjunto de los pares ordenados cuyos componentes son enteros. Para representar los números enteros se utiliza la recta numérica, y para representar el conjunto Z² se utiliza un plano cartesiano (en la imagen).

Pintura y pinceles

Sean los conjuntos T de tubos de pintura, y P de pinceles:

${\displaystyle T=\{\,}$

,

,

,

${\displaystyle \}\,}$

${\displaystyle P=\{\,}$

,

,

,

,

${\displaystyle \}\,}$

El producto cartesiano de estos dos conjuntos, T × P, contiene todos los posibles emparejamientos de pinceles y tubos de pintura. De manera similar al caso de un plano cartesiano en el ejemplo anterior, este conjunto puede representarse mediante una tabla:

Relaciones

Una relación es un vínculo o una correspondencia. En el caso de larelación matemática, se trata de la correspondencia que existe entre dos conjuntos: a cada elemento del primer conjunto le corresponde al menos un elemento del segundo conjunto.

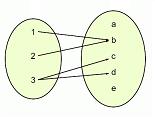
Cuando a cada elemento de un conjunto le corresponde solo uno del otro, se habla de función. Esto quiere decir que las funciones matemáticas siempre son, a su vez, relaciones matemáticas, pero que las relaciones no siempre son funciones.

En una relación matemática, al primer conjunto se lo conoce como dominio, mientras que el segundo conjunto recibe el nombre de rango o recorrido. Las relaciones matemáticas existentes entre ellos se pueden graficar en el esquema llamado plano cartesiano.

Supongamos que el dominio se llama M y el rango, N. Una relación matemática deM en N será un subconjunto del producto cartesiano M x N. Las relaciones, en otras palabras, serán pares ordenados que vinculen elementos de M con elementos de N.

Si M = {5, 7} y N = {3, 6, 8}, el producto cartesiano de M x N serán los siguientes pares ordenados:

M x N = {(5,   3), (5, 6), (5, 8), (7, 3), (7, 6), (7, 8)}

Con este producto cartesiano, se pueden definir diferentes relaciones. La relación matemática del conjunto de pares cuyo segundo elemento es menor a 7 es R = {(5, 3), (5, 6), (7, 3), (7, 6)}

Otra relación matemática que puede definirse es aquella del conjunto de pares cuyo segundo elemento es par: R = {(5, 6), (5, 8), (7, 6), (7, 8)}

ACTIVIDADES

a) Operaciones básicas
b) Plano cartesiano
c) 

Fuentes

http://definicion.de/relacion-matematica/