Grado Décimo: Ecuaciones Trigonométricas con identidades
----------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------
Ecuaciones Trigonométricas
Objetivos
- Definida una ecuación trigonométrica y modeladas varias soluciones de las mismas, cada estudiante resolverá correctamente ecuaciones trigonométricas en el intervalo [0, 2
π ) . - Haciendo uso de diferentes técnicas de solución de ecuaciones, cada estudiante determinará sin error la solución general de ecuaciones trigonométricas dadas.
Introducción
Una ecuación trigonométrica es una ecuación que contiene expresiones trigonométricas y se resuleven usando técnicas similares a las usadas en ecuaciones algebraicas, por lo que las soluciones representaran ángulos.Por ejemplo las siguientes son ecuaciones trigonométricas:
-
sen (x) = 1 -
π 3 x) = 5 -
2 (2 x − 1) = 0
Resolviendo Ecuaciones Trigonométricas
Resolveremos las ecuaciones trigonométricas en el intervalo [0, 2 ) y también de forma general.Ejemplo 1
Encontrar la solución de la ecuación,
- En el intervalo [0, ).
- En todos los números reales
Si
para todo entero n.
Ejemplo 2
Encontrar todas las soluciones de la ecuación,
Solución:
2
Análogamente con el ejemplo anterior tenemos la gráfica
Observando la imagen encontramos que los ángulos que solucionan la ecuación en [0, 2 ), son:
Como la función coseno tiene período 2 , sumamos múltiplos de este número a las soluciones anteriores.
para todo entero n.
Resolviendo Ecuaciones Trigonométricas que envuelven ángulo doble
Resolveremos las ecuaciones trigonométricas cuyas funciones trigonométricas envuelven ángulo doble, en el intervalo [0, 2 ) y también de forma general.Ejemplo 3
Encontrar todas las soluciones de la ecuación,
Solución:
Sabemos que si
sea θ = 2x luego
En grados, tenemos:
La figura muestra las soluciones de la ecuación trigonométrica coseno del ángulo doble.
Resolviendo Ecuaciones Trigonométricas mediante Factorización
Usaremos factorización para resolver ecuaciones trigonométricas.Ejemplo 4
Encontrar todas las soluciones de la ecuación,
Solución:
Las soluciones del seno son: 0,π,-π,2π,-2π,...
en general si
Por otro lado la función tangente tiene período π, así la solución de
En general, si
Finalmente, la solución de la ecuación dada son:
θ = πn y θ=
Ejemplo 5
Encontrar todas las soluciones de la ecuación,
Solución:
La ecuación trigonométrica es del tipo cuadrático
Así nuestra ecuación trigonométrica factoriza en:
2
2
en el intervalo: [0, 2 )
En general tenemos:
Ejemplo 6
Encontrar todas las soluciones de la ecuación,
Solución:
Cuando no se encuentra ninguna identidad para reducir la expresión o no se puede factorizar, es útil elevar ambos lados de la ecuación al cuadrado, pero hay que verificar la solución obtenida.
2cos
x
Verificación:
si
0+1=1 cierto.
si
0+1=-1 falso.
si x = π, tenemos:
-1+1=0 cierto
Por lo que las soluciones únicamente son: π 2 , π
En general: x La gráfica muestra la ecuación trigonométrica igualada a cero, claramente se nota que las raíces de la función representa las soluciones de la ecuación trigonométrica.
Para practicar ejercicios sobre ecuaciones tringonométricas haz click en el siguiente botón
Resumen
Ahora que has completado esta lección, eres capaz de:- Resolver ecuaciones trigonométricas en el intervalo básico [0, 2 ).
- Resolver ecuaciones trigonométricas en forma general .
----------------------------------------------------------------------------------------
Algo más de teoría
3. Demostraciones de identidades trigonométricas
Las identidades trigonómetricas son igualdades entre funciones trigonométricas que se utilizan con frecuencia. Un ejemplo de estas identidades es la identidad fundamental de la trigonometría:
En este apartado demostramos las identidades trigonométricas más importantes.
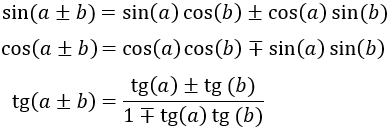 Demostramos estas fórmulas en seno, coseno y tangente de la suma y la resta de ángulos.
Demostramos estas fórmulas en seno, coseno y tangente de la suma y la resta de ángulos.
Veamos ahora el coseno, seno y tangente del ángulo mitad:
Veamos ahora sumas y restas de funciones trigonométricas:
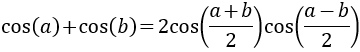
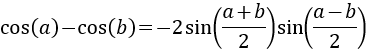 No demostramos esta identidad puesto que es similar a la resta de senos (demostrada más adelante).
No demostramos esta identidad puesto que es similar a la resta de senos (demostrada más adelante).
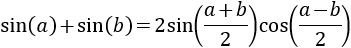 No demostramos esta identidad puesto que es similar a la suma de cosenos (demostrada anteriormente).
No demostramos esta identidad puesto que es similar a la suma de cosenos (demostrada anteriormente).
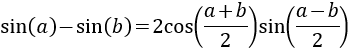
Veamos ahora productos de funciones trigonométricas escritos como sumas y restas:
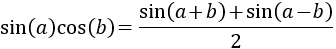
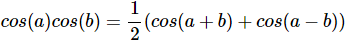
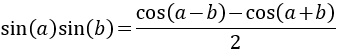
En este apartado demostramos las identidades trigonométricas más importantes.
Identidad trigonométrica fundamental
Ver demostración
Secante al cuadrado
Ver demostración
Cosecante al cuadrado
Ver demostración
Ángulos opuestos
Ver demostración
Ángulos más/menos π
Ver demostración
Suma de Ángulos
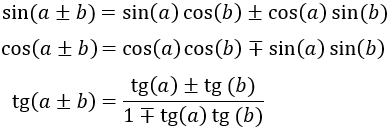
Ángulo Doble
Ver demostración
Veamos ahora el coseno, seno y tangente del ángulo mitad:
Coseno del Ángulo Medio o Ángulo Mitad
Ver demostración
Seno del Ángulo Medio o Ángulo Mitad
Ver demostración
Tangente del Ángulo Medio o Ángulo Mitad
Ver demostración
Veamos ahora sumas y restas de funciones trigonométricas:
Suma de Cosenos
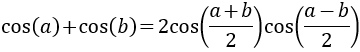
Ver demostración
Resta de Cosenos
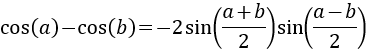
Suma de Senos
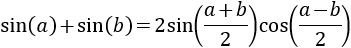
Resta de Senos
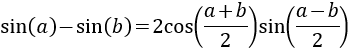
Ver demostración
Veamos ahora productos de funciones trigonométricas escritos como sumas y restas:
Producto de seno y coseno
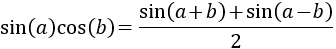
Ver demostración
Producto de cosenos
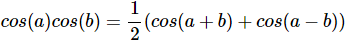
Ver demostración
Producto de senos
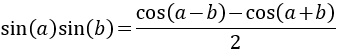
Ver demostración
Vídeos de Apoyo
Cybergrafía:







Comentarios